ベイズ推定で差分の差分法(ベイジアンDID)を行う

概要

DID(差分の差分法)は、処置群と対照群の施策前後の変化を比較し、施策による効果を推定する手法です。観察データを用いて因果効果を推定する際に有用であり、ランダム化が難しい状況などにおける選択肢の一つとなります。DIDの基本的なアプローチには、平均値の差分を計算して効果の期待値を推定する方法や、回帰モデルを用いて効果に対応する回帰係数を推定する方法があります。

しかし、これらの方法だけでは推定値に伴う不確実性を十分に評価することは困難です。そのため、推定値の点推定に加え、不確実性を分布や区間として考慮する必要があります。

本記事では、ベイズ推定を用いたDIDの実装を通じて、効果の推定とその不確実性を評価する方法をシミュレーションを交えて解説します。

なお、ベイズのシミュレーションはPyMCの3系で行われる記事が多いですが、PyMCの5系を用います。

DID(差分の差分法)の概要

差分の差分法は、その名の通り差分の差分に基づいて効果の推定値を得る手法です。イメージ図としては以下です。

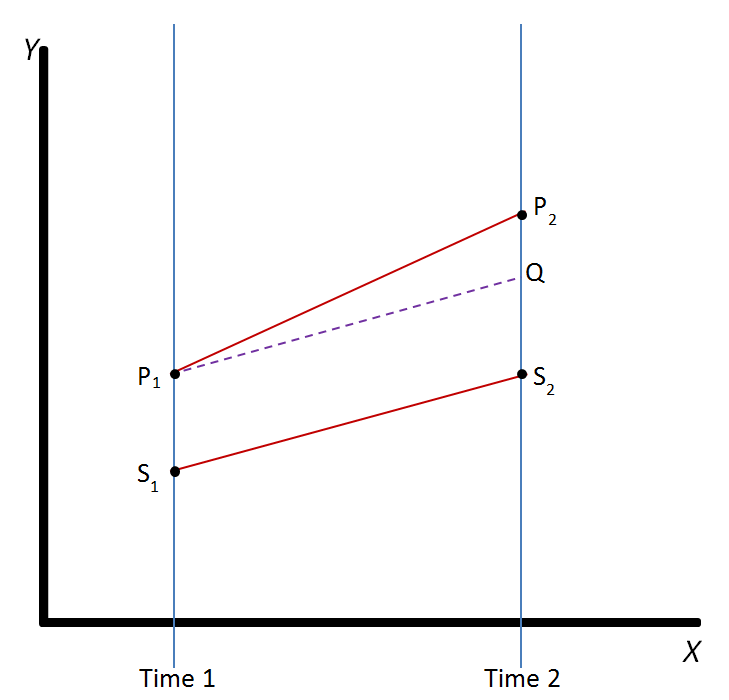
一言で言うと、効果を確かめたい処置群と同じ動きをする他の対照群があれば(パラレルトレンド仮定)、対照群の動きを処置群からキャンセルすれば効果だけを取り出せるだろう、という手法です。この考え方で、平均値の差分の差を計算するもよし、回帰モデルを構築して変化を係数に閉じ込めるもよし、です。本記事では実装にフォーカスを当てます。詳しいロジックや計算式を知りたい方はすでに先人が多くいらっしゃるので、そちらの記事や書籍をご参照ください。

• Pythonで因果推論(9)~差分の差分法(DID)による効果検証~
• 統計的因果推論(1): 差分の差分法(Difference-in-Differences)をRで回してみる

ベイジアンDID

本記事では、DIDをベイズ推定で解き、効果の事後分布を扱います。また、今回は回帰モデルでDIDを解きます。なお、パラレルトレンド仮定を含め、DIDを適用するにあたって理想的な観察データがあるという前提で議論を進めます。

問題設定

今回考える問題は、広告キャンペーンについてです。商品の購入(＝コンバージョン)を促すため、特定地域で新しい広告キャンペーンを試してその効果を測定することを考えます。

処置群を広告キャンペーンを実施した地域、対照群を広告キャンペーンを実施しなかった地域とします。キャンペーン実施前と実施後の両群のコンバージョン率を計測し、DIDによって効果を測ることを考えます。

定式化

まずはシンプルなロジスティック回帰モデルで解くように、以下を定義します。※シミュレーションがメインの記事なので、数式の説明は少し雑です。

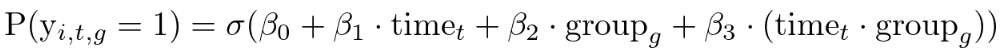
ここで、σ はロジスティック関数を示し、各変数は以下であるとします。

通常のDIDでは、これを基に最尤推定などで回帰係数の推定を行います。ここではベイズ推定を用いるため、各パラメータの事前分布を定義していきます。適切な事前分布は分からないとし、無情報に近い事前分布を採用するとします。

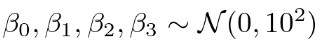
また、観測値はベルヌーイ分布に従うとします。

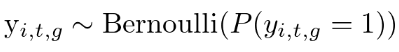
定式化ができたので、あとは事後分布を推定するだけです。ここからはこれを実装してシミュレーションしていきます。

シミュレーション

ここからはPyhonを用いてシミュレーションしていきます。まずは必要なライブラリをインポートします。

import pymc as pm
import numpy as np
from matplotlib import pyplot as plt
import arviz as az

問題設定を基に、仮に真の値が以下であったとします。

• キャンペーン前
  ・未実施地域のコンバージョン率: 10%
  ・実施地域のコンバージョン率: 20%
• キャンペーン後
  ・未実施地域のコンバージョン率: 12%
  ・実施地域のコンバージョン率: 27%

コンバージョンしたか否かの観測値が各1000サンプル得られたとします。併せて回帰式を解くために、時間、群、施策の実施を示す値もまとめておきます。

n = 1000

control_pre = np.random.binomial(n=1, p=0.10, size=n)
treatment_pre = np.random.binomial(n=1, p=0.20, size=n)
control_post = np.random.binomial(n=1, p=0.12, size=n)
treatment_post = np.random.binomial(n=1, p=0.27, size=n)

conversion = np.concatenate([control_pre, treatment_pre, control_post, treatment_post])
time = [0] * n + [0] * n + [1] * n + [1] * n
group = [0] * n + [1] * n + [0] * n + [1] * n
treated = [0] * n + [0] * n + [0] * n + [1] * n

次に前述の定式化を踏まえて事後分布を推定します。

with pm.Model() as model:
    # データ定義
    _time = pm.MutableData("time", time)
    _group = pm.MutableData("group", group)
    _treated = pm.MutableData("treated", treated)

    # 事前分布
    beta_0 = pm.Normal("beta_0", mu=0, sigma=10)
    beta_1 = pm.Normal("beta_1", mu=0, sigma=10)
    beta_2 = pm.Normal("beta_2", mu=0, sigma=10)
    beta_3 = pm.Normal("beta_3", mu=0, sigma=10)

    # ロジスティック回帰
    logit_p = beta_0 + beta_1 * _time + beta_2 * _group + beta_3 * _treated
    p = pm.Deterministic("p", pm.math.sigmoid(logit_p))

    # 事後分布推定
    y_obs = pm.Bernoulli("y_obs", p=p, observed=conversion)
    trace = pm.sample()

ここまでで各パラメータの事後分布を推定しました。

ここからは結果の確認をしていきます。各パラメータ事後分布の可視化をして推定結果を確認していきます。まずはざっくりと分布と推定の推移をみます。

az.plot_trace(trace, var_names=["beta_0", "beta_1", "beta_2", "beta_3"])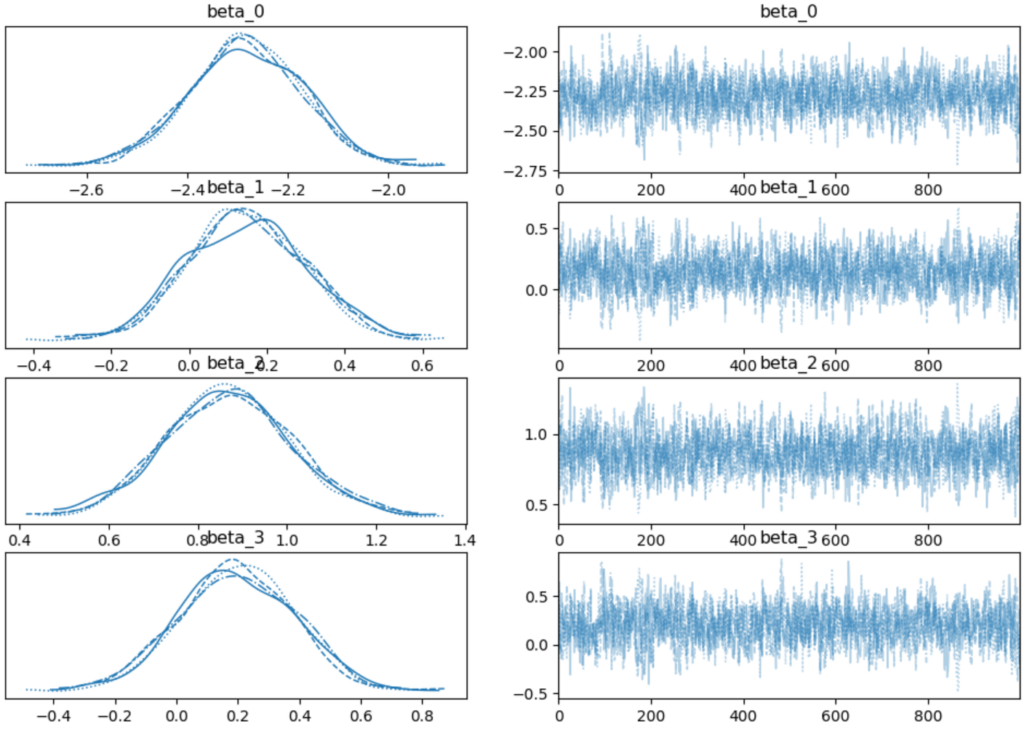

概ね滑らかで綺麗な分布であり、収束状況も問題無いことが確認できます。

パラメータの推定に問題が無かったため、事後分布に基づいて各条件における予測の分布を確認していきます。まずは分布の推定です。

# キャンペーン前、未実施地域
with model:
    pm.set_data({"time": [0], "group": [0], "treated": [0]})
    ppc_control_before = pm.sample_posterior_predictive(trace, var_names=["p"])

# キャンペーン後、未実施地域
with model:
    pm.set_data({"time": [1], "group": [0], "treated": [0]})
    ppc_control_after = pm.sample_posterior_predictive(trace, var_names=["p"])

# キャンペーン前、実施地域
with model:
    pm.set_data({"time": [0], "group": [1], "treated": [0]})
    ppc_treatment_before = pm.sample_posterior_predictive(trace, var_names=["p"])

# キャンペーン後、実施地域、キャンペーン実施無し
with model:
    pm.set_data({"time": [1], "group": [1], "treated": [0]})
    ppc_treatment_after_0 = pm.sample_posterior_predictive(trace, var_names=["p"])

# キャンペーン後、実施地域、キャンペーン実施あり
with model:
    pm.set_data({"time": [1], "group": [1], "treated": [1]})
    ppc_treatment_after_1 = pm.sample_posterior_predictive(trace, var_names=["p"])

推定した分布を描画していきます。なお、描画するものは各分布の期待値と94%信用区間とします。

fig, ax = plt.subplots(figsize=(5, 6))

az.plot_hdi(
    [0],
    ppc_control_before.posterior_predictive["p"],
    smooth=False,
    color="blue",)
control_before_expectation = np.mean(ppc_control_before.posterior_predictive["p"])
ax.plot([0], control_before_expectation, 'o', color="blue")

az.plot_hdi(
    [1],
    ppc_control_after.posterior_predictive["p"],
    smooth=False,
    color="blue",)
control_after_expectation = np.mean(ppc_control_after.posterior_predictive["p"])
ax.plot([1], control_after_expectation, 'o', color="blue")

ax.plot(
    [0, 1],
    [control_before_expectation, control_after_expectation],
    color="blue",
    linestyle="--",)

az.plot_hdi(
    [0],
    ppc_treatment_before.posterior_predictive["p"],
    smooth=False,
    color="red",)
treatment_before_expectation = np.mean(ppc_treatment_before.posterior_predictive["p"])
ax.plot([0], treatment_before_expectation , 'o', color="red")

az.plot_hdi(
    [1],
    ppc_treatment_after_1.posterior_predictive["p"],
    smooth=False,
    color="red",)
treatment_after_expectation = np.mean(ppc_treatment_after_1.posterior_predictive["p"])
ax.plot([1], treatment_after_expectation, 'o', color="red")

ax.plot(
    [0, 1],
    [treatment_before_expectation, treatment_after_expectation],
    color="red",
    linestyle="--",)

az.plot_hdi(
    [1],
    ppc_treatment_after_0.posterior_predictive["p"],
    smooth=False,
    color="pink",)
treatment_after_expectation_0 = np.mean(ppc_treatment_after_0.posterior_predictive["p"])
ax.plot([1], treatment_after_expectation_0, 'o', color="pink")

ax.plot(
    [0, 1],
    [treatment_before_expectation, treatment_after_expectation_0],
    color="pink",
    linestyle="--",)

ax.set_xticks([0, 1])
plt.show()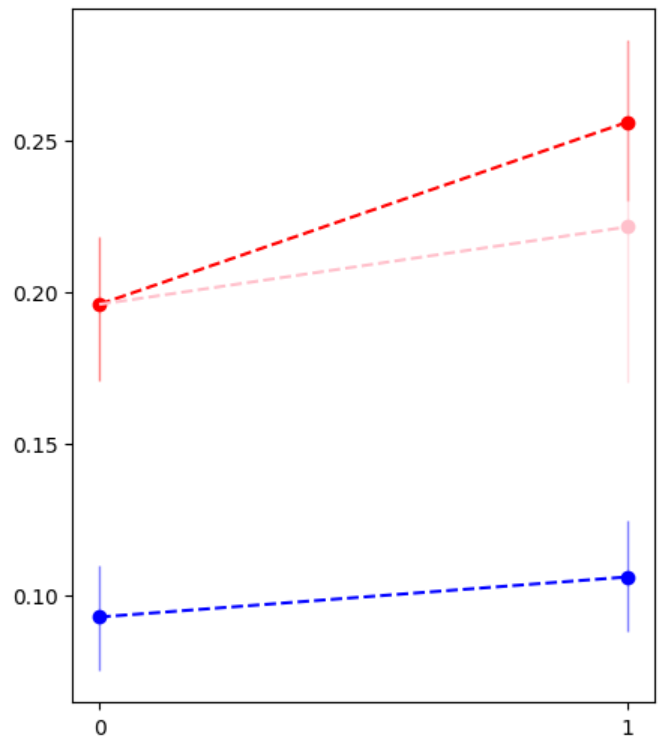

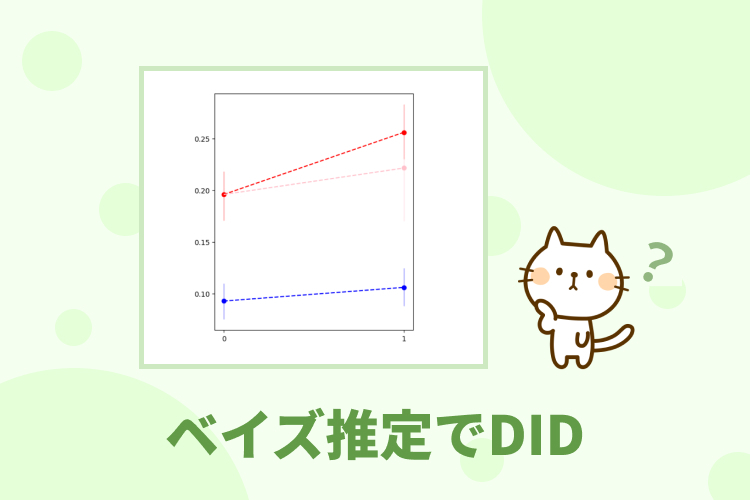
青がキャンペーン未実施、赤がキャンペーン実施、ピンクが仮に赤の地域でキャンペーンを実施しなかった場合の推定結果です。

これを見ると、ピンクと比べて赤が確かに向上してそうに見えるので、キャンペーンによる効果があったのではないかと期待できます。

これを定量的に確かめるために、効果の大きさの分布を推定し、可視化します。

effect_distribution = ppc_treatment_after_1.posterior_predictive["p"] - ppc_treatment_after_0.posterior_predictive["p"]

effect_mean = effect_distribution.mean()
effect_hdi = az.hdi(effect_distribution)

az.plot_posterior(effect_distribution)
plt.title("キャンペーンによる効果の分布")
plt.xlabel("コンバージョン率の変化")
plt.ylabel("密度")
plt.show()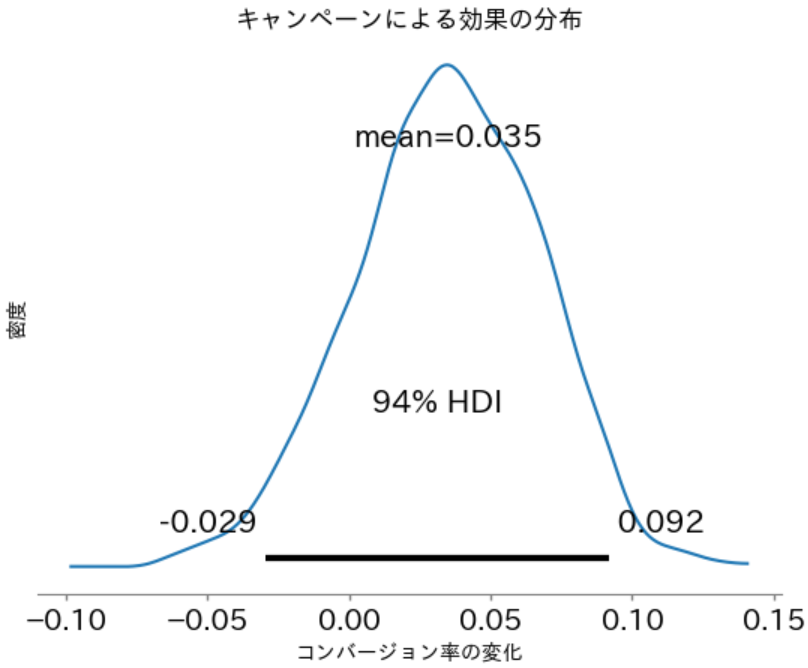

94%信用区間が[-0.029, 0.092]で期待値が 0.035 なので、プラスの効果が期待できそうです。

最後に効果が0以上である確率を計算します。

print(f"効果が0以上である確率:{(effect_distribution >= 0).mean():.3f}")

結果は 0.848 となり、85%程度の確率でキャンペーンによる効果があったと言えます。

なお、この確率についてはキャンペーンの効果に関わる回帰係数の分布を見ることでも確認できます。

az.plot_posterior(trace, var_names=["beta_3"])

beta_3_samples = trace.posterior["beta_3"].values.flatten()
prob_beta_3_positive = (beta_3_samples >= 0).mean()
print(f"効果が0以上である確率: {prob_beta_3_positive:.3f}")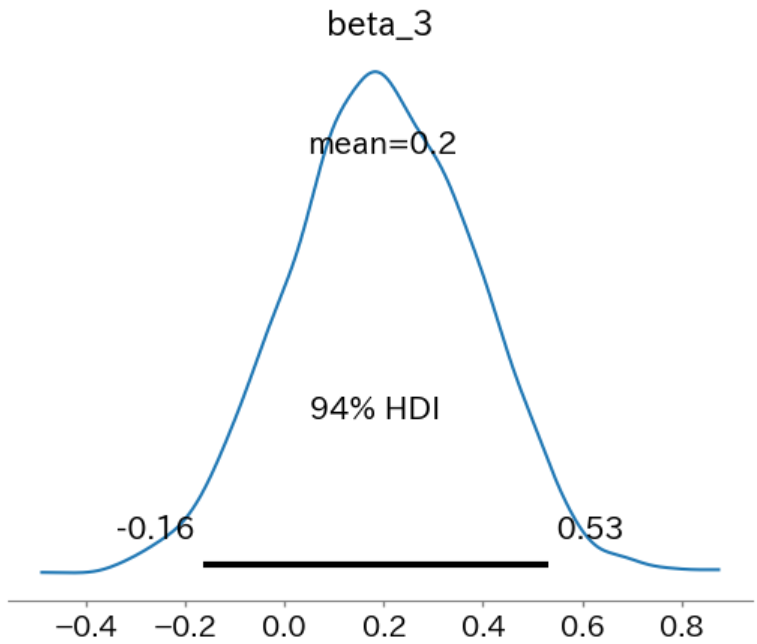

94%信用区間が[-0.16, 0.53]、期待値が0.2、係数が0以上の確率が 0.848 となり、上記の結果と相違ない結果となりました。

ここまでで、DIDにおいて効果の測定を不確実性を考慮しながら推定を行いました。効果を確率的に評価することができて使いやすいですね。

ベイジアンDIDのまとめ

本記事ではベイズ推定によるDIDを実施しました。事後分布で不確実性や効果の大きさを評価でき、直感的な解釈ができるので非常に便利ですね。

なお、今回のようなシンプルなモデリングであれば通常のロジスティック回帰でも恐らく不確実性を含めほぼ同じ結果が得られるでしょう。一方でベイズ推定を用いることで、階層ベイズで柔軟なモデリングが可能であったり、事前分布が適切に設定できればより有益な結果が得られたりと、問題設定次第で強力な手段になります。(事前分布を適切に設定するなんてできるのか、という話は触れないでおきます。)

参考文献

途中で紹介していますが、DIDに関しての解説記事は分かりやすいものが多くあり、特に以下の二つはかなり勉強になるかと思います。

• Pythonで因果推論(9)~差分の差分法(DID)による効果検証~
• 統計的因果推論(1): 差分の差分法(Difference-in-Differences)をRで回してみる

また、DIDについては下記の書籍が分かりやすく、学ぶのに非常に良いです。

• Pythonで学ぶ効果検証入門
• 効果検証入門〜正しい比較のための因果推論/計量経済学の基礎
• 岩波データサイエンス Vol.3

ベイズ統計の導入ついては下記の書籍が分かりやすいです。

• 完全独習 ベイズ統計学入門
• Pythonでスラスラわかる ベイズ推論「超」入門

留意点

本シミュレーションは単純な問題設定の下で、パラレルトレンド仮定や他介入が存在しないなどの強い仮定があるためうまくいっていると言えます。特にパラレルトレンド仮定は非常に強い仮定であり、かつDIDにおいて重要な前提となるので注意してください。

また、事前分布について、今回のシミュレーションにおいては問題の仮定を踏まえて無情報とみなせるような分布を用いました。まとめで少し触れましたが、事前分布の選択が意思決定を大きく左右しますので、事前分布の設計は慎重に行う必要があります。

統計学を学びたい方へのおすすめ

統計検定2級 or 3級取得までマンツーマンで教えるサービスを提供しています。

統計を学び、資格取得を目指す方はまずは無料の初回コンサルをお申込みください。

サービス詳細はこちら