ベイジアンABテストで必要なサンプルサイズを見積もる

概要
サンプルサイズを見積もる方針
ベイズ推定によるシミュレーション
ベイジアンABテストにおけるサンプルサイズ見積もりのまとめ
1. 参考文献
留意点
統計を学びたい方へ

概要

ABテストを行うにあたって、ベイズ推定は非常に強力なツールです。特にサンプルサイズが十分でない場合でも、リスクとスピードのバランスが取りやすく、頻度論的な仮説検定よりもビジネス的な意思決定に適しています。

一方で、サンプルサイズがいくらでも良い訳ではなく、ベイズ推定においてもサンプルサイズを考慮することは重要です。

サンプルサイズが少ない場合、頻度論的な仮説検定では有意差がないと判断される一方、ベイズ推定では有意性が不十分な確率が得られることになります。つまり、A(or B)の方が良い確率が55%、といったような結果です。

もちろん状況によりますが、55%の確率でAが良いと言われてもAにすべきかBにすべきか迷ってしまいます。従って、意思決定に十分な確率を得るためにサンプルサイズを大きくする必要があります。

一方で、サンプルの収集には時間や費用などのコストがかかります。例えば、WebデザインのABテストにおいて、判断に十分なインプレッション(≒サンプル)を得るのに1年かかります、だと話になりません。

これを踏まえ、判断に十分な結果が得られる見込みの最低限のサンプルサイズを見積もれると、ABテストの計画が立てやすいと言えます。

本記事においては、ベイジアンABを行う際のサンプルサイズの見積もりについて考え、そのシミュレーションを行います。

サンプルサイズを見積もる方針

頻度論における仮説検定では、サンプルサイズは有意水準、検出力、期待できる効果量から解析的に計算することがある程度可能です。(参考: https://bellcurve.jp/statistics/course/12769.html )

一方で、ベイズ推定では事後分布を求める際に柔軟な事前分布や尤度を設定できるため、頻度論的仮説検定と比べて分布の仮定が緩いです。この柔軟性のために事後分布を綺麗に求められない場合が多く、サンプルサイズの解析的計算が難しくなります。そのため、サンプルサイズの推定にはシミュレーションを活用するのが一般的です。

これを踏まえ、大きな方向性として解釈可能な指標を設定し、その閾値を満たすサンプルサイズをシミュレーションで探索します。

指標については、αエラーやβエラーに基づく指標、ベイズファクターに基づく指標、これらを基にしたリスク(or メリット)の期待値などが考えられます。適切な指標の議論はさまざまですが、本記事においては効果量が見込める際にそれを正しく検出できるか否か、という観点でサンプルサイズの見積もりを行います。

ベイズ推定によるシミュレーション

ここからはシミュレーションの詳細に入っていきます。まずは必要なライブラリをインポートします。

import japanize_matplotlib
from matplotlib import pyplot as plt
import numpy as np
import pandas as pd
from scipy.stats import beta
import seaborn as sns

問題設定

比較するものは施策Aと施策Bとし、それらの施策は成功か失敗かのいずれかの観測値を得るものとします。例えば、Web広告AとBをそれぞれ入稿してそれがインプレッション(試行)されるたびにコンバージョン(成功)するか、という塩梅です。また、問題の簡略化のために理想的なランダムサンプリングができていると仮定し、データに意図せぬバイアスは無いとします。

この広告AとBを配信してどちらが良いのかを判定することを考えますが、この時どれぐらいの回数表示させれば(サンプルサイズをどれぐらいと見積もれば)差があると判定できるだろうか、ということを考えます。

シミュレーションデータの用意

シミュレーションとして、広告Aと広告Bの真のコンバージョン率が以下だったとします。

広告A: 2.5%
広告B: 5%

広告Bの方がコンバージョン率が高いので、広告Bの方が良いという判断を観測値から下したい、と言えます。広告のコンバージョンは発生するか否かの0か1を取る、以上の仮定が無いため、広告のコンバージョン数は二項分布に従うと考えます。

上記を踏まえ、以下でシミュレーション用のデータを生成します。

p_A, p_B = 0.025, 0.05
successes_A = np.random.binomial(n, p_A)
successes_B = np.random.binomial(n, p_B)

サンプルサイズのシミュレーション

今回データから推定するものは「各広告のコンバージョン率がいくつか」であり、「その差がどの程度あるのか」です。

これが分かれば、どちらの広告がどの程度優れていそうだから広告A(or B)を選ぶことが可能です。今回は95%の確率でA(or B)の方が少しでも優れている、という結果が得られたら良し悪しの判断するとします。

また、上記の結果がサンプルサイズをずらしていくとどのように変化するかを求めて、妥当なサンプルサイズがいくつか、を考えていきます。

サンプルサイズを無数に探索することは困難なので、10～10000までをいい塩梅で刻んでシミュレーションを行います。また、各サンプルサイズについて1度だけシミュレーションを行う場合、たまたま上(下)振れてしまうということが十分想定できるので、各サンプルサイズに対してシミュレーションを1000回行うとします。

trials = 1000
sample_sizes = [10, 20, 50, 80, 100, 200, 500, 800, 1000, 2000, 5000, 8000, 10000]

この1000回の結果の事後分布を集計することで、それぞれのサンプルサイズでどれぐらい正しい判断が行えたのか、を計測します。

なお、コンバージョン率の分布には二項分布の共役事前分布であるベータ分布を採用し、α=1, β=1の無情報事前分布とします。

alpha_prior, beta_prior = 1, 1

ここからシミュレーションしていきます。各サンプルサイズに対して1000回の事後分布の推定を行い、Bが勝つ確率を集計していきます。

win_rate_dists = []
for n in sample_sizes:
    win_rate_dist = []
    for i in range(trials):
        successes_A = np.random.binomial(n, p_A)
        successes_B = np.random.binomial(n, p_B)

        posterior_A = beta(alpha_prior + successes_A, beta_prior + n - successes_A)
        posterior_B = beta(alpha_prior + successes_B, beta_prior + n - successes_B)

        samples_A = posterior_A.rvs(50000)
        samples_B = posterior_B.rvs(50000)

        diff_samples = samples_B - samples_A
        win_rate_B = np.mean(diff_samples > 0)
        win_rate_dist.append(win_rate_B)
    win_rate_dists.append(win_rate_dist)

そして、Bが勝つ確率がどのような分布になっているかを確認します。

df = pd.DataFrame(np.array(win_rate_dists).T, columns=np.array(sample_sizes))

plt.figure(figsize=(10, 6))
sns.violinplot(data=df, palette="Blues")
plt.title("Bが勝つ確率の分布")
plt.ylabel("")
plt.grid(axis="y")
plt.show()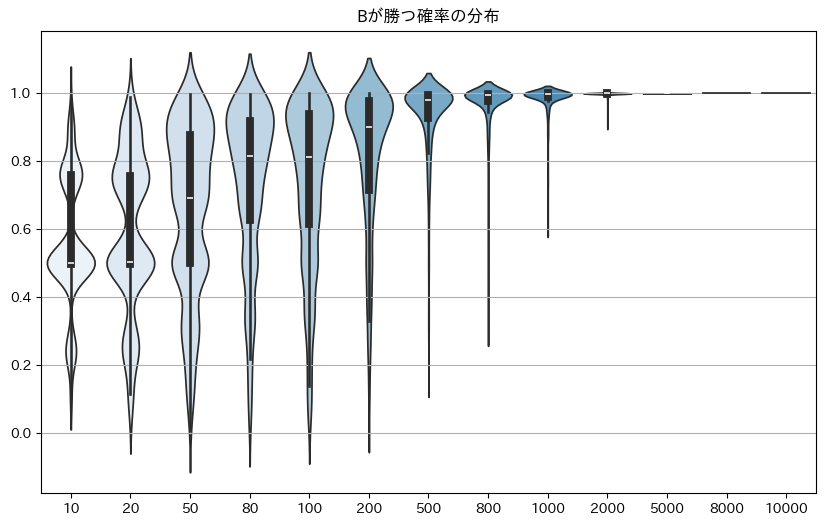

これを確認すると、サンプルサイズが増えるにつれて確かにBが勝つと判定されたケースが増えていることが分かります。

また今回の問題設定では、いずれかが95%以上の確率で勝つ場合判断を下すとしていたため、Bが勝つ確率が95%を超えるサンプルがどれぐらいあったかを集計していきます。

significance_level = 0.95

true_positive_rates = []
for win_rate_dist in win_rate_dists:
    true_positive_rate = np.mean(np.array(win_rate_dist) >= significance_level)
    true_positive_rates.append(true_positive_rate)

plt.figure(figsize=(8, 6))
plt.plot(sample_sizes, true_positive_rates, marker='o', linestyle='-', color='blue', label='Bの方が良いと判定できた割合')
plt.legend()
plt.xlabel("サンプルサイズ")
plt.ylabel("Bの方が良いと判定できた割合")
plt.xscale("log")
plt.grid()
plt.show()

ここまでで、サンプルサイズとBの方が良いと判定できた割合の対応が取れました。例えば、800サンプルでは約84%、2000サンプルでは99%以上の確率で正しい判断が可能と言えます。

ここからの意思決定は定性判断になりますが、安全に倒したい場合は2000サンプルぐらいは必要であると見積もればよいですし、800サンプルぐらいでも正しく判定できる確率はそれなりに高いと言ってよいのでは無いでしょうか。

ベイジアンABテストにおけるサンプルサイズ見積もりのまとめ

ここまでで、ベイジアンABにおけるサンプルサイズの見積もりのシミュレーションを行いました。

事前にサンプルサイズを見積もることで、必要な時間やコストを把握し、意思決定に役立てることができますね。

参考文献

本記事のようなベイズ統計を学ぶ際には下記の書籍が非常に良いと思います。

完全独習ベイズ統計学入門: https://amzn.to/41ag4Wa

Pythonでスラスラわかるベイズ推論「超」入門: https://amzn.to/3VcQ08Y

前者はかなり優しく、導入の書籍として非常に良いです。その後、後者の方を用いながら実装しながら学んでいくのが良いと思います。

留意点

本シミュレーションは単純な問題設定の下で分布が綺麗に定まる、という前提があるためうまくいっていると言えます。

今回は二項分布とその共役事前分布であるベータ分布を用いたため、MCMCのような重たいシミュレーションは不要でした。一方で、指標によってはもっと複雑な分布を用いる必要があると思います。その場合は計算量が非常に多くなり計算が終わらなかったり、分布の推定時に収束するか否かが不安定であったりで、同様のシミュレーションは難しい可能性は十分あります。